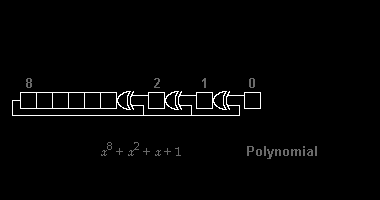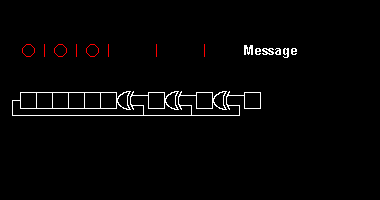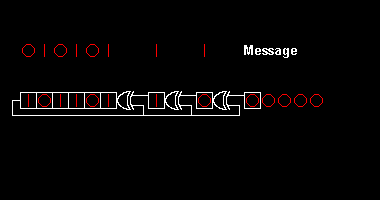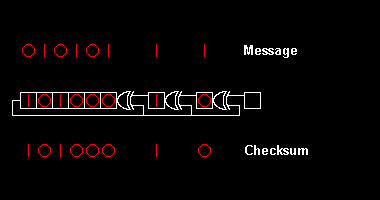Here is the logic behind the condition that must be satisfied:
Step 1: Let’s consider the card number as 1802909582961827
Step 2: As of now, just consider first 15 digits i.e., 180290958296182|7
Step 3: Now beginning from the left, start with the first number, take every second number and multiply it by 2 as shown here:
Starting from the first i.e., 1 and taking every second number, we will get the following numbers: 1 0 9 9 8 9 1 2
1 * 2 = 2
0 * 2 = 0
9 * 2 = 18
9 * 2 = 18
8 * 2 = 16
9 * 2 = 18
1 * 2 = 2
2 * 2 = 4
Step 4: Sum up the digits if the multiplication results in a 2 digit number. i.e., 18 => 1 + 8 = 9
This will give us all the result in a single digit number.
So, we get : 2,0,9,9,7,9,2,4
Step 5: Now, Sum up all the single digits and all the digits left in the card number.
i.e., 2+0+9+9+7+9+2+4 + 8+2+0+5+2+6+8 = 73
Add the sum together. Now, what must be added to the sum obtained so that it is divisible by 10? In this case, it is 7
So, 73+ 7 = 80 which is divisible by 10.
This last digit so obtained is called as Checksum digit.
That’s the logic behind credit/debit card numbers.